xkcd-np
Mix.install([
:fixpoint,
{:kino, "~> 0.10.0"}
])
Logger.configure(level: :notice)
defmodule ServingTablesHelpers do
def visualize_route(optimal_route, distances, tables, table_coordinates) do
len = length(tables)
IO.puts(
Enum.map_join(optimal_route, " \u2b95 ", fn idx -> "[" <> Enum.at(tables, idx) <> "]" end)
)
IO.puts("\n")
IO.puts("Start from where you are, and follow the directions :-)")
## Create a route visualization
route_graph =
Enum.reduce(
0..(len - 1),
Graph.new(),
fn idx, acc ->
v1 = Enum.at(optimal_route, idx)
v2 = Enum.at(optimal_route, idx + 1)
weight = Enum.at(distances, v1) |> Enum.at(v2)
Graph.add_edge(acc, v1, v2, len: weight, label: " #{weight} ")
end
)
{:ok, route_graph_content} = Graph.to_dot(route_graph)
route_graph_content =
Enum.reduce(0..(len - 1), route_graph_content, fn idx, acc ->
{x, y} = Enum.at(table_coordinates, idx)
replace_params = "[label=#{Enum.at(tables, idx)}; pos=\"#{x},#{y}!\"]"
# || "[label=#{Enum.at(tables,idx)}]"
String.replace(acc, "[label=#{idx}]", replace_params)
end)
dir = System.tmp_dir!()
dot_file = Path.join(dir, "xkcd_route_graph.dot")
png_file = Path.join(dir, "xkcd_route.png")
File.write(dot_file, route_graph_content)
System.cmd("neato", [
"-Tpng:quartz",
dot_file,
"-o",
png_file,
"-Nfontsize=20",
"-Nfontcolor=red",
"-Nshape=diamond",
"-Efontcolor=blue",
"-Efontsize=20"
])
## Render with Kino
content = File.read!(png_file)
Kino.Image.new(content, "image/png")
end
def distances_from_coordinates(coordinates) do
len = length(coordinates)
for i <- 0..(len - 1) do
{x1, y1} = Enum.at(coordinates, i)
for j <- 0..(len - 1) do
{x2, y2} = Enum.at(coordinates, j)
:math.sqrt(:math.pow(x1 - x2, 2) + :math.pow(y1 - y2, 2)) |> round()
end
end
end
endHow do you solve with Constraint Programming?
xkcd, as always, helps us to explain things :-)
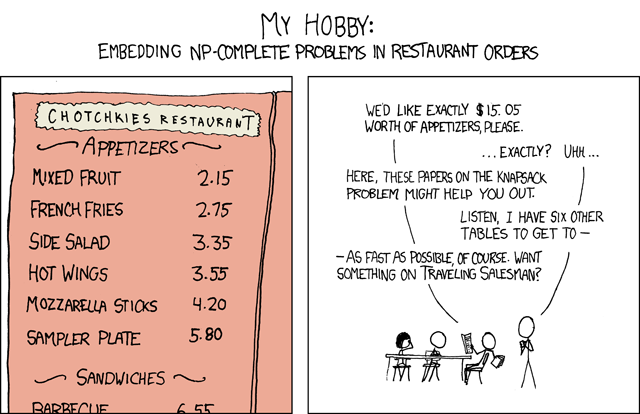
Solving customer request for appetizers
First, create a model for the problem.
Meaning we declare the decision variables and the constraints over them.
- The decision variables are the quantities per appetizer
- The single constraint is that the total price of the appetizers is exactly what the customers require.
defmodule XKCD.NP.Appetizers do
alias CPSolver.IntVariable, as: Variable
alias CPSolver.Model
import CPSolver.Variable.View.Factory
alias CPSolver.Constraint.Sum
def model() do
appetizers = [
{:mixed_fruit, 215},
{:french_fries, 275},
{:side_salad, 335},
{:hot_wings, 355},
{:mozarella_sticks, 420},
{:sampler_plate, 580}
]
total = 1505
## We want to find the quantities for each appetizer...
quantities =
Enum.map(appetizers, fn {name, price} ->
Variable.new(0..div(total, price), name: name)
end)
### ...such that the total price will be exactly as the customers ask
###
priced_quantities =
Enum.zip(quantities, appetizers)
|> Enum.map(fn {q_var, {_name, price}} -> mul(q_var, price) end)
Model.new(
quantities,
[Sum.new(total, priced_quantities)]
)
end
def print_solutions(solver_results) do
(Enum.map_join(solver_results.solutions, "\n OR \n", fn sol ->
sol
|> Enum.zip(solver_results.variables)
|> Enum.reject(fn {q, name} -> q == 0 || is_reference(name) end)
|> Enum.map_join(", ", fn {q, name} ->
IO.ANSI.red() <> "#{name} : #{IO.ANSI.blue()}#{q}"
end)
end) <> IO.ANSI.reset())
|> IO.puts()
end
endOnce we have a model, we feed it to a solver.
alias XKCD.NP.Appetizers
## Solve
{:ok, res} = CPSolver.solve(Appetizers.model())
## Present results
Appetizers.print_solutions(res)
IO.puts("Solver status: #{res.status}")
That’s it! Two solutions are available.
Serving tables as fast as possible
We want to minimize the total distance the waiter walks to serve the tables.
We will use a model that solves Travelling Salesman Problem:
https://github.com/bokner/fixpoint/blob/main/lib/examples/tsp.ex
alias CPSolver.Examples.TSP
import ServingTablesHelpers
tables = ["Table1", "Table2", "Table3", "Table4", "Table5", "Table6", "Table7"]
table_coordinates = [{4, 7}, {5, 5}, {7, 2}, {1, 5}, {1, 1}, {8, 4}, {11, 5}]
distances = distances_from_coordinates(table_coordinates)
model = TSP.model(distances)
{:ok, result} = CPSolver.solve(model, search: TSP.search(model), space_threads: 8)
optimal_solution = result.solutions |> List.last()
optimal_route = TSP.to_route(optimal_solution, model)
visualize_route(optimal_route, distances, tables, table_coordinates)result.solutions{result.statistics.elapsed_time, optimal_route, result.objective}
